Bài đăng phổ biến
-
TẢI XUỐNG MÁY Tải qua SMS soạn tin: DL 5G4828 gửi 8009 (500đ) Sòng Bài 2012 : Du hành tới LasVegas tham gia thi đấu các game Tá lả,Tiến...
-
Tiểu luận "Đối chiếu động từ "ăn" trong tiếng Việt và tiếng Anh" Cùng với danh từ, động từ là hai thực từ cơ bản nhất tr...
-
Mô tả lỗi: Tiếng Việt: Xin vui lòng nhập giá trị callback method Tiếng Anh: Please enter a valid callback method Hãy nhớ Upload các file lê...
-
Chị Tôn Phượng Cầm, 47 tuổi ở Khu tự trị Nội Mông, Trung Quốc mắc một căn bệnh kỳ lạ, lưng đột nhiên sưng to giống như phần mai con rùa khiế...
-
Cồn khô, cồn nước, hiện được các hộ gia đình, các quán ăn sử dụng thay thế bếp gas mini khi nấu ăn. Tuy nhiên, nếu không biết cách nấu, các...
-
Nếu bạn đã cảm thấy nhàm chán với màn hình khởi động mặc định của chiếc điện thoại, bạn muốn tạo một phong cách riêng trên chiếc điện thoại ...
-
Bài viết này được thực hiện theo yêu cầu của bạn xtranfor55 trong bài viết Cuộn ảnh nền và bản đồ (Map Scrolling). Tôi sẽ hướng dẫn cách là...
-
Notes: dùng trong word để trang trí bìa báo cáo tốt nghiệp, tiểu luận. http://www.mediafire.com/?cpb572e73m7bq50 chúc các bạn làm báo cáo tố...
-
Tính đến 6-8, Việt Nam ghi nhận 1.043 trường hợp dương tính với cúm A/H1 N1 Cục Y tế dự phòng và Môi trường (Bộ Y tế) cho biết, ngày 6-8, V...
Home » Vật lý
Bất đẳng thức Côsi (Cơ bản)
5 thg 8, 2012
MỘT SỐ BÀI TOÁN CHỨNG MINH BẤT ĐẲNG THỨC (CƠ BẢN) |
Nhắc lại:
* BĐT Côsi áp dụng cho hai số không âm:
(1)
- Cách viết tương đương:. (2)
Dấuxẩy ra khi và chỉ khi
.
* Chú ý: Với hai số thực tùy ý, ta có:
-(Vì
.
* Một số kết quả thường dùng:
.
Thật vậy, vì 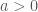 nên
nên  . Áp dụng BĐT (2) cho hai số này ta được:
. Áp dụng BĐT (2) cho hai số này ta được:
 .
.
.
Thật vậy, vì 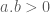 nên
nên  . Áp dụng BĐT (2) cho hai số này ta được:
. Áp dụng BĐT (2) cho hai số này ta được:
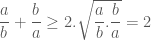 .
.
————————————
MỘT SỐ BÀI TẬP
Bài 1: Bài toán thuận.
Chứng minh rằng với mọita có:
.
Dấu đẳng thức (dấu bằng) xảy ra khi nào ?
Hướng dẫn:
Trong bài toán này có chứa hai số hạng dạng nghịc đảo. Vì đã có số hạng nên phần còn lại phải biểu diễn thành thừa số của
nên phần còn lại phải biểu diễn thành thừa số của 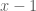 . Vậy ta phải viết lại vế trái như sau:
. Vậy ta phải viết lại vế trái như sau:
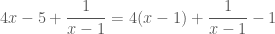 (*)
(*)
Vì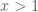 nên
nên  .
.
Áp dụng bất đẳng thức Côsi (2) cho 2 số dương , ta có:
, ta có:

Hay . (**)
. (**)
Kết hợp với (*), suy ra:
 .
.
Vậy (đpcm)
(đpcm)
Theo (**), dấu đẳng thức xảy ra

 (do
(do  )
)
 .
.
——-
Trong bài toán này có chứa hai số hạng dạng nghịc đảo. Vì đã có số hạng
Vì
Áp dụng bất đẳng thức Côsi (2) cho 2 số dương
Hay
Kết hợp với (*), suy ra:
Vậy
Theo (**), dấu đẳng thức xảy ra
——-
Bài 2: Bài toán ngược của dạng Bài toán 1.
Chứng minh rằng
Hướng dẫn:
Khác với bài 1, vế trái bài này có dạng tích, nên ta cần chú ý một dạng tương đường của BĐT (1) là . (3)
. (3)
Quay lại bài tập này, với mọi![x\in [1; 5] x\in [1; 5]](http://s0.wp.com/latex.php?latex=x%5Cin+%5B1%3B+5%5D&bg=ffffff&fg=4e4e4e&s=0) thì
thì 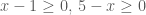 . Vậy áp dụng BĐT (3) cho hai số không âm này ta có:
. Vậy áp dụng BĐT (3) cho hai số không âm này ta có:
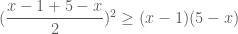
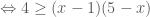 . (đpcm)
. (đpcm)
Dấu “=” xảy ra .
.
Khác với bài 1, vế trái bài này có dạng tích, nên ta cần chú ý một dạng tương đường của BĐT (1) là
Quay lại bài tập này, với mọi
Dấu “=” xảy ra
——————
BÀI TẬP TỰ GIẢI.
Chứng minh rằng:
1..
2.
3. Với mọi góc, ta có:
.
4..
5..
—————




Comments[ 0 ]
Đăng nhận xét